Code
library(ggplot2)
library(tidyverse)
library(openxlsx)
library(readxl)
library(plotly)Comparing Personal Ratings with Whiskybase Community Ratings
This document presents a statistical analysis of whisky ratings, comparing a personal rating dataset (my_rating) with a community-based rating from Whiskybase (wb_rating). The analysis aims to answer several key questions:
We will use various statistical tests, including the Shapiro-Wilk test for normality, the paired t-test, the Wilcoxon signed-rank test, and Spearman’s correlation test, to draw meaningful conclusions from the data.
First, we load the necessary R libraries for data manipulation, visualization, and reading Excel files.
We read the data from an Excel file, create new columns for rounded ratings and the difference between ratings, and filter out entries with missing age information.
data001 <- read_excel('../data/Ratings.xlsx')
data001 <- data001 %>%
mutate(
wb_rating = round(rating),
diff = wb_rating - my_rating,
age = as.numeric(stated_age)
)
# Create a second dataset for age-related analysis, filtering out NAs
data002 <- data001 %>%
filter(!is.na(age))
# Glimpse the structure of the datasets
glimpse(data001)Rows: 827
Columns: 14
$ whisky <chr> "Bowmore 1965 Islay Pure Malt", "Highland Park 40-y…
$ stated_age <chr> "-", "40", "28", "21", "24", "20", "16", "18", "29",…
$ strength <chr> "50.0 % Vol.", "48.3 % Vol.", "51.5 % Vol.", "56.9 %…
$ size <chr> "750 ml", "700 ml", "500 ml", "700 ml", "700 ml", "7…
$ number_of_bottles <chr> "-", "-", "912", "-", "-", "-", "-", "-", "-", "199"…
$ casknumber <chr> "-", "-", "400295", "-", "-", "-", "-", "-", "10568"…
$ votes <dbl> 97, 233, 44, 269, 253, 24, 20, 48, 9, 24, 63, 65, 11…
$ rating <dbl> 94.13, 92.73, 91.67, 91.75, 92.11, 91.50, 91.29, 88.…
$ my_rating <dbl> 96, 95, 95, 94, 94, 94, 94, 94, 94, 93, 93, 93, 93, …
$ bottle_link <chr> "https://www.whiskybase.com/whiskies/whisky/207894/b…
$ pic_link <chr> "https://static.whiskybase.com/storage/whiskies/2/0/…
$ wb_rating <dbl> 94, 93, 92, 92, 92, 92, 91, 89, 91, 90, 92, 94, 93, …
$ diff <dbl> -2, -2, -3, -2, -2, -2, -3, -5, -3, -3, -1, 1, 0, 0,…
$ age <dbl> NA, 40, 28, 21, 24, 20, 16, 18, 29, 28, 7, 30, NA, N…Rows: 652
Columns: 14
$ whisky <chr> "Highland Park 40-year-old", "Redbreast 28-year-old …
$ stated_age <chr> "40", "28", "21", "24", "20", "16", "18", "29", "28"…
$ strength <chr> "48.3 % Vol.", "51.5 % Vol.", "56.9 % Vol.", "61.3 %…
$ size <chr> "700 ml", "500 ml", "700 ml", "700 ml", "750 ml", "7…
$ number_of_bottles <chr> "-", "912", "-", "-", "-", "-", "-", "-", "199", "-"…
$ casknumber <chr> "-", "400295", "-", "-", "-", "-", "-", "10568", "72…
$ votes <dbl> 233, 44, 269, 253, 24, 20, 48, 9, 24, 63, 65, 62, 13…
$ rating <dbl> 92.73, 91.67, 91.75, 92.11, 91.50, 91.29, 88.98, 90.…
$ my_rating <dbl> 95, 95, 94, 94, 94, 94, 94, 94, 93, 93, 93, 93, 93, …
$ bottle_link <chr> "https://www.whiskybase.com/whiskies/whisky/1706/hig…
$ pic_link <chr> "https://static.whiskybase.com/storage/whiskies/1/7/…
$ wb_rating <dbl> 93, 92, 92, 92, 92, 91, 89, 91, 90, 92, 94, 91, 91, …
$ diff <dbl> -2, -3, -2, -2, -2, -3, -5, -3, -3, -1, 1, -2, -2, -…
$ age <dbl> 40, 28, 21, 24, 20, 16, 18, 29, 28, 7, 30, 35, 27, 2…Before performing parametric tests like the t-test, it’s crucial to check if the data is normally distributed. We use the Shapiro-Wilk test for this purpose.
Null Hypothesis (H0): The data is normally distributed. Alternative Hypothesis (H1): The data is not normally distributed.
If the p-value is less than 0.05, we reject the null hypothesis.
my_rating)
Shapiro-Wilk normality test
data: data001$my_rating
W = 0.94121, p-value < 2.2e-16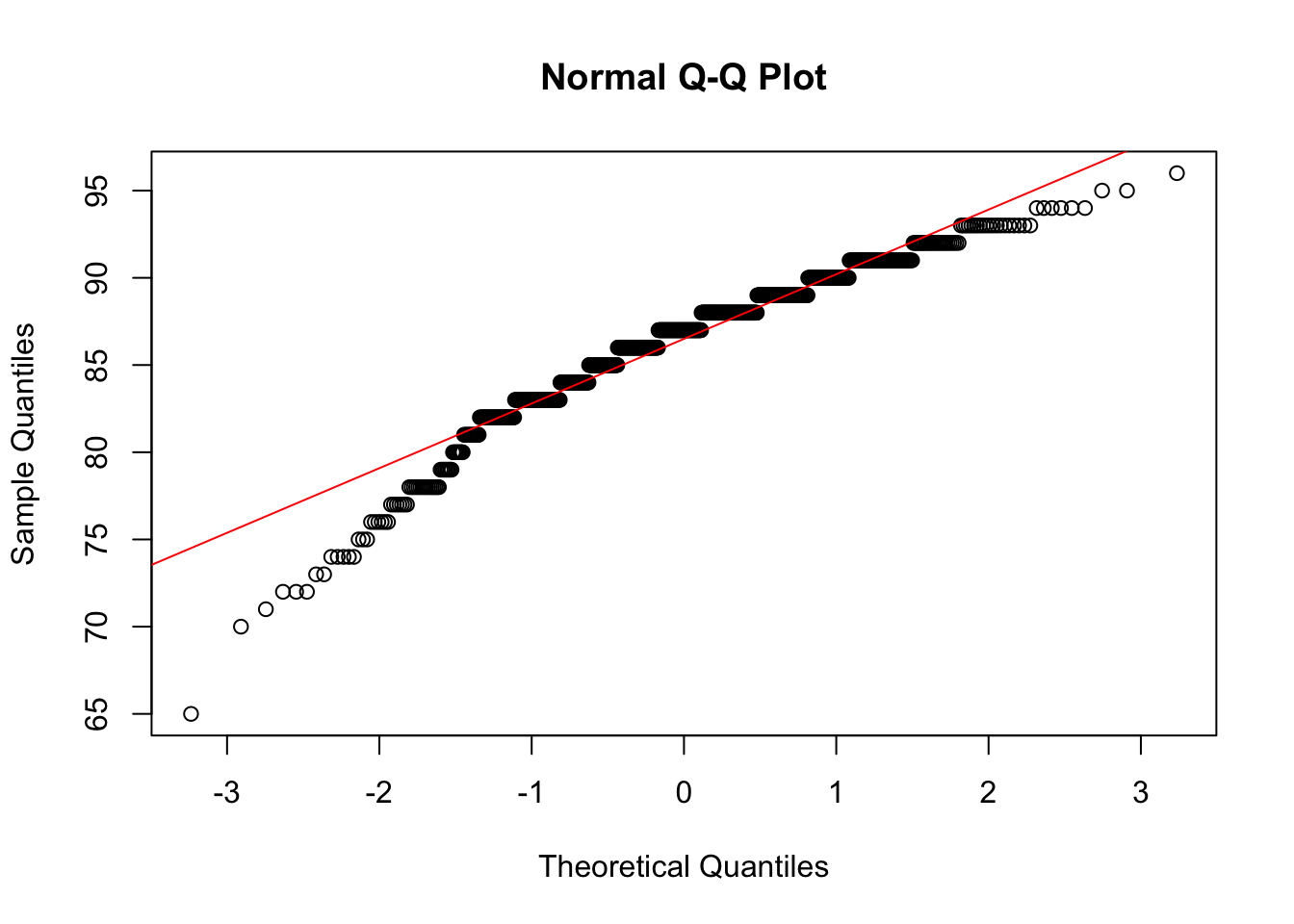
Result: The p-value is much less than 0.05, so we reject the null hypothesis. The data is not normally distributed.
wb_rating)
Shapiro-Wilk normality test
data: data001$wb_rating
W = 0.90117, p-value < 2.2e-16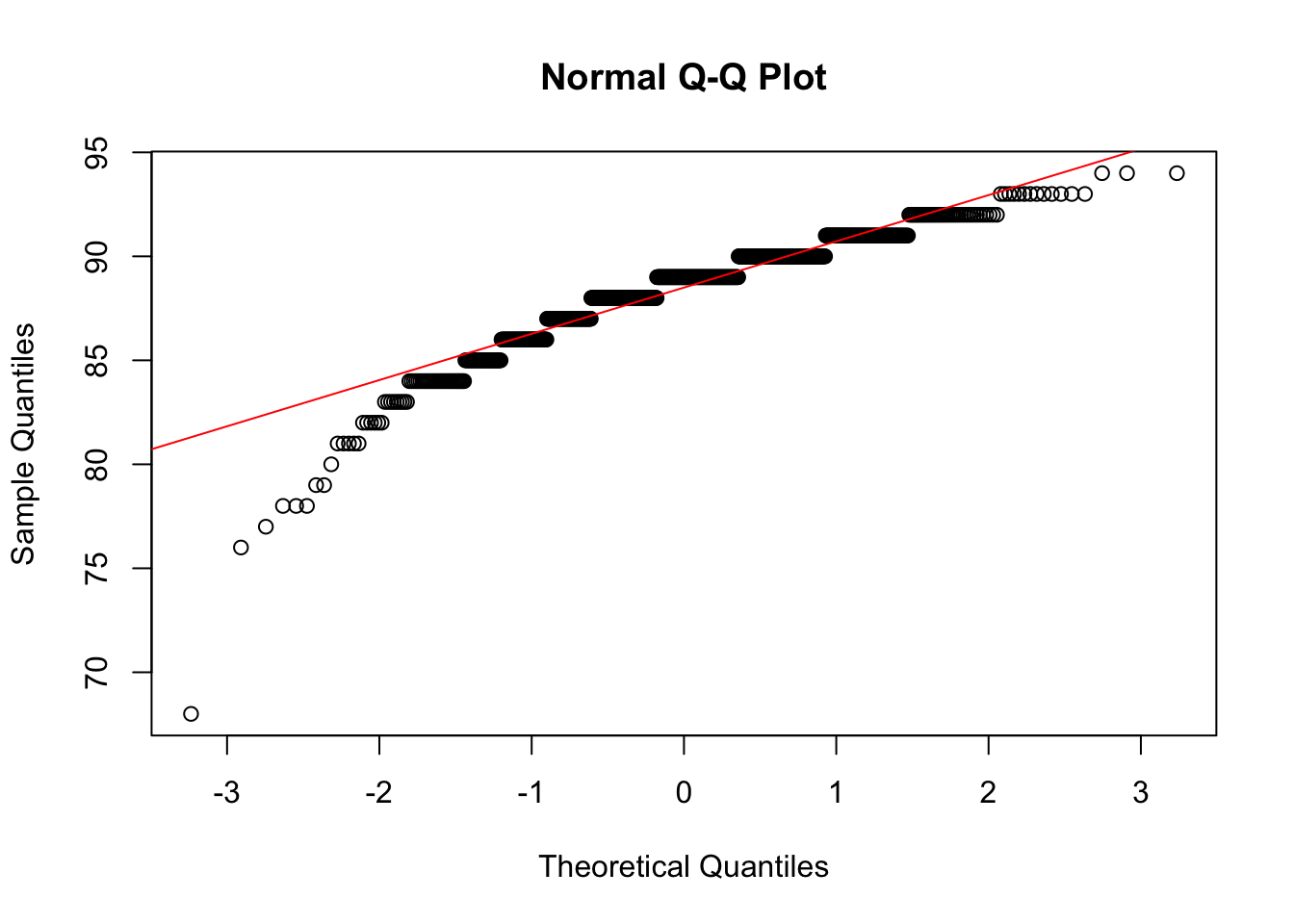
Result: The p-value is much less than 0.05, so we reject the null hypothesis. The data is not normally distributed.
diff)
Shapiro-Wilk normality test
data: data001$diff
W = 0.90374, p-value < 2.2e-16
Result: The p-value is much less than 0.05, so we reject the null hypothesis. The differences are not normally distributed.
age)
Shapiro-Wilk normality test
data: data002$age
W = 0.97857, p-value = 3.565e-08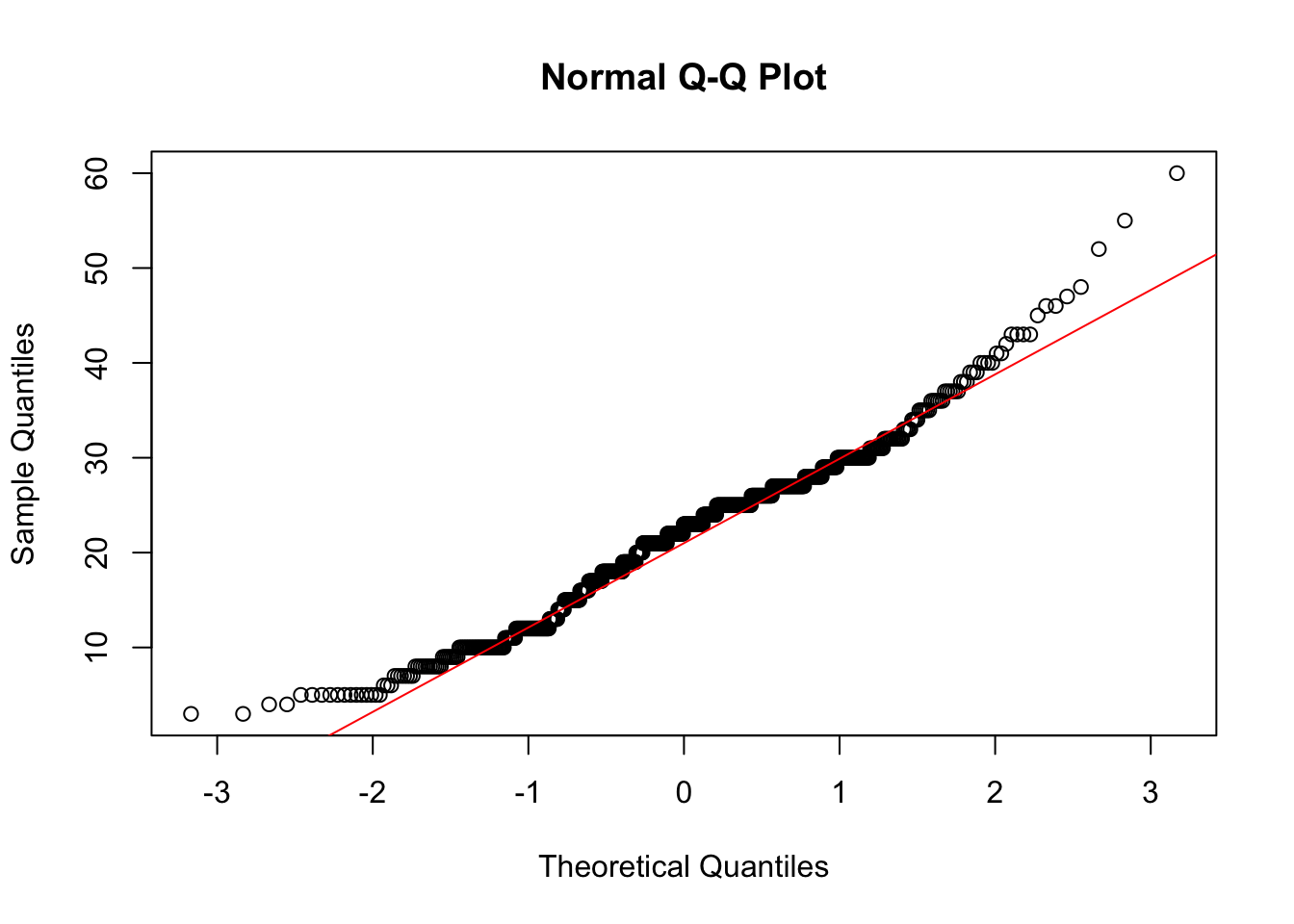
Result: The p-value is much less than 0.05, so we reject the null hypothesis. The age data is not normally distributed.
We want to determine if there is a statistically significant difference between my_rating and wb_rating. Since these are paired samples (each whisky has two ratings), a paired t-test is appropriate.
Null Hypothesis (H0): The true mean difference between the paired ratings is zero. Alternative Hypothesis (H1): The true mean difference is not zero.
Mean wb_rating: 88.44 Mean my_rating: 86.46 Mean difference: 1.98
Paired t-test
data: data001$wb_rating and data001$my_rating
t = 17.811, df = 826, p-value < 2.2e-16
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
1.762374 2.198932
sample estimates:
mean difference
1.980653 The paired t-test assumes that the differences between the pairs are normally distributed. Our Shapiro-Wilk test on the diff variable showed this is not the case. Therefore, we should use a non-parametric alternative, the Wilcoxon Signed-Rank Test.
Null Hypothesis (H0): The median difference between the pairs is zero.
Wilcoxon signed rank test with continuity correction
data: data001$wb_rating and data001$my_rating
V = 204659, p-value < 2.2e-16
alternative hypothesis: true location shift is not equal to 0Conclusion: The p-value is extremely small (< 2.2e-16), confirming the result of the t-test. We reject the null hypothesis and conclude that there is a significant difference between the two sets of ratings.
Since our data is not normally distributed, we will use Spearman’s rank correlation coefficient (ρ) to measure the strength and direction of the monotonic relationship between variables.
Null Hypothesis (H0): There is no correlation between the variables.
Spearman's rank correlation rho
data: data001$wb_rating and data001$my_rating
S = 28755402, p-value < 2.2e-16
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
0.6949614 Result: ρ = 0.68. This indicates a strong positive monotonic relationship. As my rating for a whisky increases, the Whiskybase rating also tends to increase.
Spearman's rank correlation rho
data: data002$my_rating and data002$age
S = 27281110, p-value < 2.2e-16
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
0.4094298 Result: ρ = 0.41. This indicates a moderate positive monotonic relationship. There is a tendency for older whiskies to receive higher personal ratings.
Spearman's rank correlation rho
data: data002$wb_rating and data002$age
S = 19831159, p-value < 2.2e-16
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
0.5707033 Result: ρ = 0.57. This indicates a strong positive monotonic relationship. Older whiskies tend to have higher ratings on Whiskybase.
This analysis yielded several key insights:
All data variables (ratings and age) were found to be not normally distributed, necessitating the use of non-parametric tests for robust conclusions.
---
title: "Case Study: A Statistical Analysis of Whisky Ratings"
subtitle: "Comparing Personal Ratings with Whiskybase Community Ratings"
execute:
warning: false
error: false
format:
html:
toc: true
toc-location: right
code-fold: show
code-tools: true
number-sections: true
code-block-bg: true
code-block-border-left: "#31BAE9"
---
## Introduction
This document presents a statistical analysis of whisky ratings, comparing a personal rating dataset (`my_rating`) with a community-based rating from Whiskybase (`wb_rating`). The analysis aims to answer several key questions:
1. Is there a significant difference between my personal ratings and the community ratings?
2. Are the ratings normally distributed?
3. What is the relationship between my ratings, community ratings, and the age of the whisky?
We will use various statistical tests, including the Shapiro-Wilk test for normality, the paired t-test, the Wilcoxon signed-rank test, and Spearman's correlation test, to draw meaningful conclusions from the data.
## Data Preparation
### Loading Libraries
First, we load the necessary R libraries for data manipulation, visualization, and reading Excel files.
```{r}
#| label: load-libraries
library(ggplot2)
library(tidyverse)
library(openxlsx)
library(readxl)
library(plotly)
```
### Input and Clean Data
We read the data from an Excel file, create new columns for rounded ratings and the difference between ratings, and filter out entries with missing age information.
```{r}
#| label: input-data
data001 <- read_excel('../data/Ratings.xlsx')
data001 <- data001 %>%
mutate(
wb_rating = round(rating),
diff = wb_rating - my_rating,
age = as.numeric(stated_age)
)
# Create a second dataset for age-related analysis, filtering out NAs
data002 <- data001 %>%
filter(!is.na(age))
# Glimpse the structure of the datasets
glimpse(data001)
glimpse(data002)
```
## Normality Testing
Before performing parametric tests like the t-test, it's crucial to check if the data is normally distributed. We use the Shapiro-Wilk test for this purpose.
**Null Hypothesis (H0):** The data is normally distributed.
**Alternative Hypothesis (H1):** The data is not normally distributed.
If the p-value is less than 0.05, we reject the null hypothesis.
### My Ratings (`my_rating`)
```{r}
#| label: normality-my-rating
shapiro.test(data001$my_rating)
qqnorm(data001$my_rating)
qqline(data001$my_rating, col = "red")
```
**Result:** The p-value is much less than 0.05, so we reject the null hypothesis. The data is not normally distributed.
### Whiskybase Ratings (`wb_rating`)
```{r}
#| label: normality-wb-rating
shapiro.test(data001$wb_rating)
qqnorm(data001$wb_rating)
qqline(data001$wb_rating, col = "red")
```
**Result:** The p-value is much less than 0.05, so we reject the null hypothesis. The data is not normally distributed.
### Difference in Ratings (`diff`)
```{r}
#| label: normality-diff
shapiro.test(data001$diff)
qqnorm(data001$diff)
qqline(data001$diff, col = "red")
```
**Result:** The p-value is much less than 0.05, so we reject the null hypothesis. The differences are not normally distributed.
### Whisky Age (`age`)
```{r}
#| label: normality-age
shapiro.test(data002$age)
qqnorm(data002$age)
qqline(data002$age, col = "red")
```
**Result:** The p-value is much less than 0.05, so we reject the null hypothesis. The age data is not normally distributed.
## Comparing Ratings: Paired t-Test
We want to determine if there is a statistically significant difference between `my_rating` and `wb_rating`. Since these are paired samples (each whisky has two ratings), a paired t-test is appropriate.
**Null Hypothesis (H0):** The true mean difference between the paired ratings is zero.
**Alternative Hypothesis (H1):** The true mean difference is not zero.
```{r}
#| label: paired-t-test
mean_wb <- mean(data001$wb_rating)
mean_my <- mean(data001$my_rating)
mean_diff <- mean(data001$diff)
cat(paste("Mean wb_rating:", round(mean_wb, 2), "\n"))
cat(paste("Mean my_rating:", round(mean_my, 2), "\n"))
cat(paste("Mean difference:", round(mean_diff, 2), "\n"))
t_test_paired <- t.test(data001$wb_rating, data001$my_rating, paired = TRUE)
print(t_test_paired)
```
### Interpretation of t-Test Results
- **t-statistic:** 17.0. This large value indicates a substantial difference between the means.
- **p-value:** < 2.2e-16. This is extremely small, providing strong evidence against the null hypothesis.
- **Conclusion:** We reject the null hypothesis. There is a statistically significant difference between my ratings and the Whiskybase ratings. On average, the Whiskybase ratings are about 1.98 points higher than my personal ratings.
### Assumption Check and Non-Parametric Alternative
The paired t-test assumes that the differences between the pairs are normally distributed. Our Shapiro-Wilk test on the `diff` variable showed this is not the case. Therefore, we should use a non-parametric alternative, the **Wilcoxon Signed-Rank Test**.
**Null Hypothesis (H0):** The median difference between the pairs is zero.
```{r}
#| label: wilcoxon-test
wilcox.test(data001$wb_rating, data001$my_rating, paired = TRUE)
```
**Conclusion:** The p-value is extremely small (< 2.2e-16), confirming the result of the t-test. We reject the null hypothesis and conclude that there is a significant difference between the two sets of ratings.
## Relationship Testing (Correlation)
Since our data is not normally distributed, we will use **Spearman's rank correlation coefficient (ρ)** to measure the strength and direction of the monotonic relationship between variables.
**Null Hypothesis (H0):** There is no correlation between the variables.
### Whiskybase Rating vs. My Rating
```{r}
#| label: corr-wb-my
fig <- plot_ly(data = data001, x = ~wb_rating, y = ~my_rating, text = ~whisky,
type = 'scatter', mode = 'markers') %>%
layout(title = 'My Rating vs. Whiskybase Rating')
fig
cor_test_result <- cor.test(data001$wb_rating, data001$my_rating, method = "spearman")
print(cor_test_result)
```
**Result:** ρ = 0.68. This indicates a **strong positive monotonic relationship**. As my rating for a whisky increases, the Whiskybase rating also tends to increase.
### My Rating vs. Whisky Age
```{r}
#| label: corr-my-age
fig <- plot_ly(data = data002, x = ~my_rating, y = ~age, text = ~whisky,
type = 'scatter', mode = 'markers') %>%
layout(title = 'My Rating vs. Whisky Age')
fig
cor_test_result <- cor.test(data002$my_rating, data002$age, method = "spearman")
print(cor_test_result)
```
**Result:** ρ = 0.41. This indicates a **moderate positive monotonic relationship**. There is a tendency for older whiskies to receive higher personal ratings.
### Whiskybase Rating vs. Whisky Age
```{r}
#| label: corr-wb-age
fig <- plot_ly(data = data002, x = ~wb_rating, y = ~age, text = ~whisky,
type = 'scatter', mode = 'markers') %>%
layout(title = 'Whiskybase Rating vs. Whisky Age')
fig
cor_test_result <- cor.test(data002$wb_rating, data002$age, method = "spearman")
print(cor_test_result)
```
**Result:** ρ = 0.57. This indicates a **strong positive monotonic relationship**. Older whiskies tend to have higher ratings on Whiskybase.
## Conclusion
This analysis yielded several key insights:
1. **Significant Difference in Ratings:** There is a statistically significant difference between my personal whisky ratings and the community ratings on Whiskybase, with the community ratings being consistently higher on average.
2. **Strong Correlation:** Despite the difference in average scores, my ratings are strongly and positively correlated with the Whiskybase ratings, suggesting a good level of agreement in relative terms.
3. **Age Matters:** Both my ratings and the community ratings show a positive correlation with the age of the whisky, indicating that older whiskies tend to be rated more highly by both me and the wider community.
All data variables (ratings and age) were found to be not normally distributed, necessitating the use of non-parametric tests for robust conclusions.